新学期たのしいね
全国の「おたまじゃくし」のみなさん。そして、全国の小中学生のみなさん。
いよいよ新学期ですね。
日に日に夕暮(ゆうぐ)れがはやくなってきていますね。
こんにちは。こんばんわ。ボク「かえるのクー」といいます。
さて、今回は、神経(しんけい)の接続(せつぞく)を「モデル」で表してみます。モデルとは「模型」(もけい)みたいなものだよ。いろんな洋服の似合う、かっこいいおねーさんも「モデル」ということがあるけど、今回はそちらではないよ。
「神経接続」をモデルであらわしたものをニューラルネットワークといいます。NN(えぬえぬ)と略(りゃく)すこともあるよ。
ニューラルネットワーク(NN)を説明するとき、すこしだけ専門用語(せんもんようご)がでてくるけど、一度イメージを覚(おぼ)えてしまえばそんなに難(むずか)しくないと思います。
ニューラルネットワーク(NN)は神経接続をまねて、これ以上できないくらい単純(たんじゅん)にしたものです。
接続の形は似ているけど、実物(じつぶつ)のニューロンとはそんなにも似(に)ていないかもしれません。
どんなところが似ていて、どんなところが違うのか興味(きょうみ)があったらこの記事(きじ)を読んでみてください。(すこし長いけど最後まで読んでくれたらうれしいな)
「ノード」と「エッジ」。聞きなれないけどボクタチノコト覚えてね。
では今日は自己符号化器(じごふごうかき)の「部品」(ぶひん)でもある「ノード」くんに説明してもらいましょう。「ノード」くんどうぞ
|
|
「ノード」くん自画像 |
こんにちは。ボクハ「ノード」といいます。ノードの説明をするね。
「ネットワーク」は点と線で表すことが多いです。ネットワークとは、いろんなものがつながっていることです。
ボク「ノード」ノ友達の「エッジ」くんを紹介します。
|
|
「エッジ」 (ある高名な画家による肖像画)
こんにちは。「エッジ」です。 「ノード」とつながって なにかを伝えるのが役目です。 |
点の部分のことを「ノード」、線の部分のことを「エッジ」といいます。
「ノード」と「エッジ」でネットワークを表します。「ノード」をパソコンやルータ装置やハブ装置、「エッジ」を「LAN線」にみたてる魔法を使えば、「LANやクラウド」をあらわせます。人に見たてれてば、親子関係や血縁をあらわせそうです。つながりをもったあらゆるものを表します。
比較しよう
実際の「神経接続」と先輩たちが考えた「ニューラルネットワーク(NN)」とを比べてみましょう。
図 神経ネットワークとニューラルネットワーク(NN)
|
|
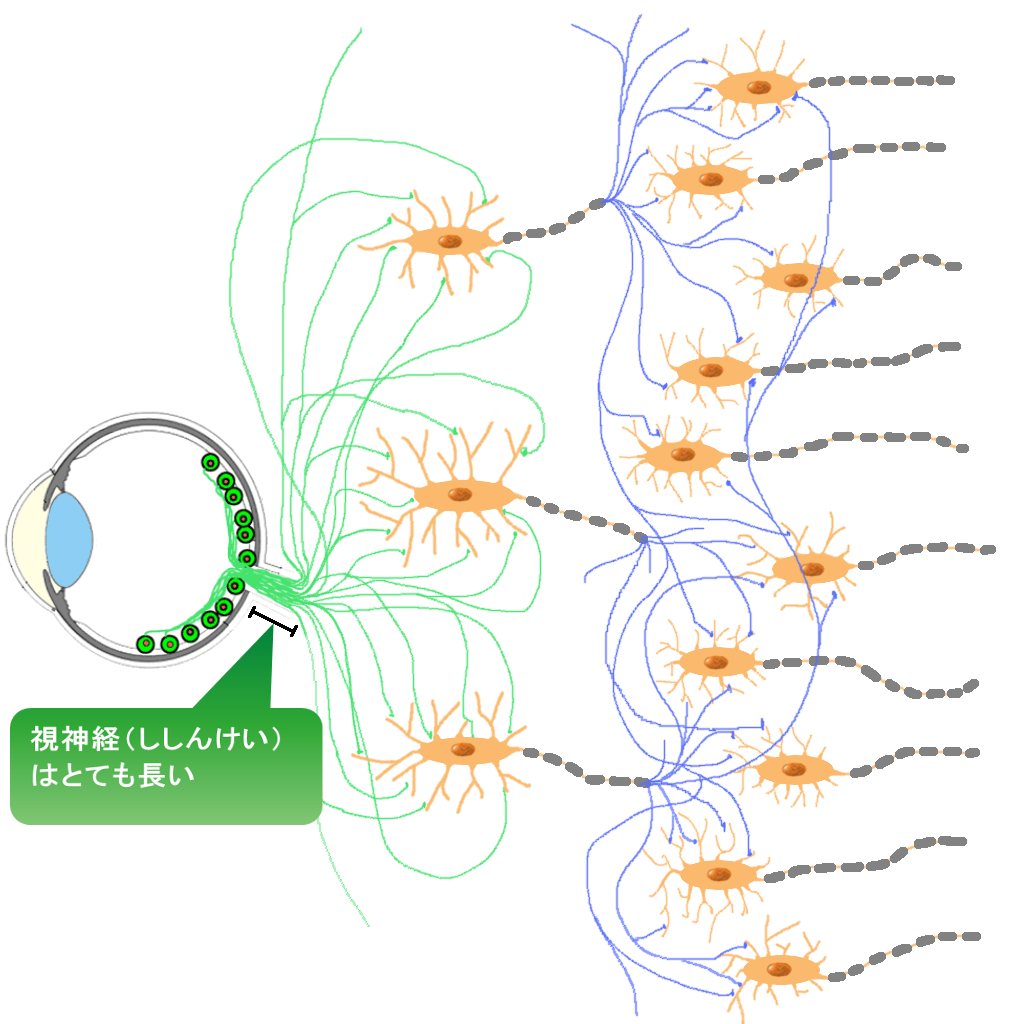
神経接続 目の網膜(もうまく)にある視神経(ししんけい)の光を受けて反応する情報が、頭のうしろにある視覚野(しかくや)とよばれる部分にまでつながっているよ。 |
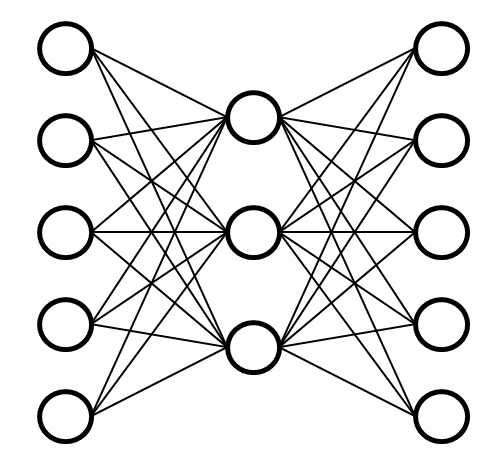 |
ニューラルネットワーク(NN) まあるい形の部分が「ノード」 線でつながっている部分が「エッジ」です。 |
接続の形は似ていますが、神経細胞の「樹状突起」(じゅじょうとっき)や「軸索」(じくさく)に相当するものはありません。「神経」と「ノード」の「反応のしかた」も実はまったく違います。
にているところ
| 似ているところ | 説明 |
|---|---|
| 接続のしかた |
接続でよく(強く)つながっている部分と弱い部分がある。 神経細胞ではいくつもつながっていたり、よく反応する状態になります。 ニューラルネットワークは接続の強さを「重み(W)」ということもあります。 |
| 元気のでかた |
しきい値があって、一定以上にならないと神経/ノードは元気にならない。 神経細胞では自律的に調整する部分もありますが、しきい値のようなところがあり、そこを超えれば、発火(はっか)する(興奮(こうふん)すること、元気になることです。もちろん火はでません) ニューラルネットでは熱くなり方(性格:活性化化関数)にもよりますが、「バイアス(b)」で実質的なしきい値を調整します。しきい値といってもニューラルネットではゆるやかな場合が多いです。 |
案外にているところはすくないのかも。でも、接続の強さ(「重み」)としきい値(「バイアス」で調整)が似ていることはとっても重要です。
違うところ
| 違うところ | 神経接続(しんけいせつぞく) | ニューラルネットワーク(NN) |
|---|---|---|
| 信号の伝わり方 |
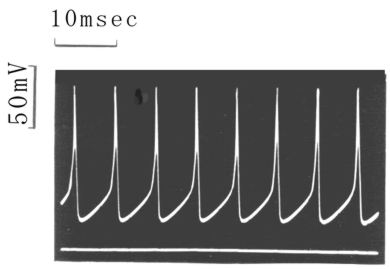
神経はパルス信号(波形)が伝わります。こんな波です。(とがった波をパルスというよ)
|
計算値が伝わります。計算時間以外は瞬間(しゅんかん)に伝わります。 |
| 時間について |
神経は時間が関係ある (波が最初から終わりまで伝わる時間や遅れがあります。) |
時間が関係ない(考慮していない) 計算時間以外は遅れがない |
|
活性化(かっせいか) について |
比較的極端(きょくたん)に元気になります。(活性化) |
使う関数 f(性格)によりますが、 神経細胞とくらべ「なだらか」なものがつかわれることが多いです。
|
|
活性化(かっせいか) の量について (どれくらい元気か) |
パルスの数や密度(みつど:こみぐあい)であらわします。 | 計算値が大きいか小さいかであらわします |
| 学習のしかた | まだまだ未解明(みかいめい)な部分が多いです。自己組織化(じこそしきか)と反省(フィードバック)と階層的最適化(どこをとってもエコ)かもしれません。「重ね合わせ」で同時に処理しているという先生もいます。 |
いろいろな方法が考えられています。誤差逆伝搬法(ごさぎゃくでんぱんほう)*1とよばれる方法など、たくさん考えられています。 |
| 接続 | シナプスという部分で化学物質(かがくぶっしつ)をやりとりすることによりつたえます。まれに電気的につないでいる部分もあります。(普通の神経の接続は電気的な接続ではないです) |
「ノード」の層の間は全部「エッジ」でつながっている(層の考え方はあとからでてくるよ) つなげたくない部分は「重み(w)」をゼロにする。(「重み(w)」もあとからでてくるよ) |
| 部分とまとまり | 入力の樹状突起から本体の細胞核(さいぼうかく)、軸索、出力のシナプスがワンセットです。 |
「ノード」と「エッジ」からできる。 それぞれは別々にあつかう。 |
細かい部分はまだまだ違います。
ニューラルネットワーク(NN)
ニューラルネットワーク(NN)は情報を〇(ノード)と/(エッジ)の結合で学習し表現します。
では数字を学習(入力して圧縮して復元して出力)するニューラルネットワーク(NN)をつくってみましょう。
読み込む数字(画像が28×28で全部で784個あるとします)
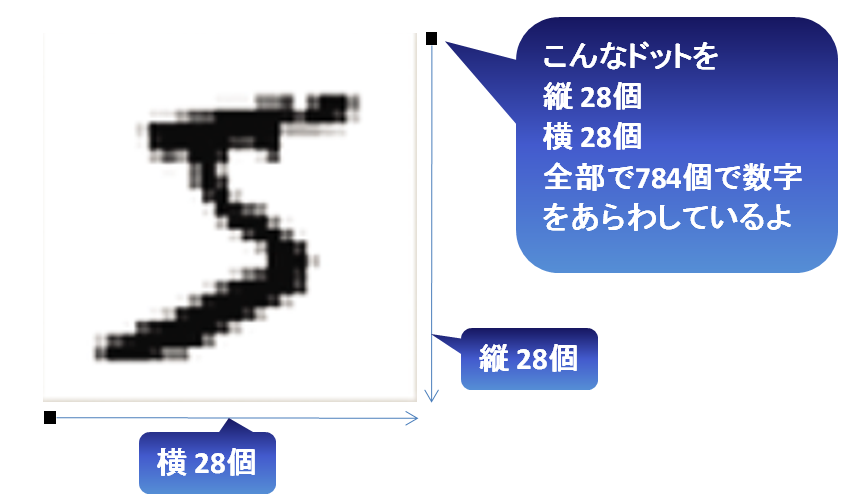
こんな図形を学習するよ。
つながりをあらわす材料
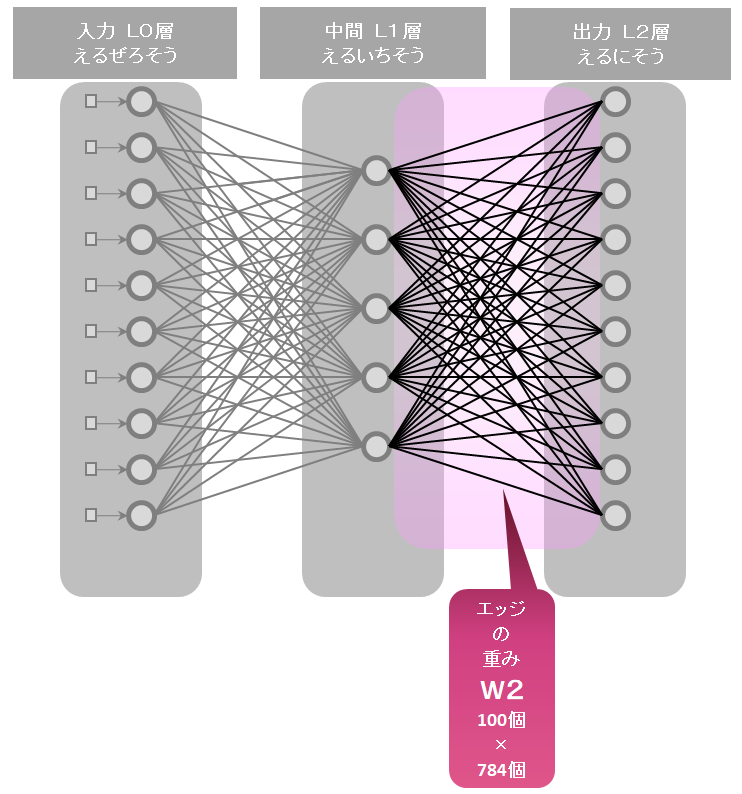
(1)784個の入力用〇(ノード)
入力の画像をよみこむもの(目とかセンサーに相当するもの)
28×28の画像をもとにするけど、ドットを全部1列にならべます。画像の縦横のつながりはまったく関係なくなります。単に点が784個並んでいるだけです。(この点は重要です。点は画像でも、音の波(の点)、なんでもOKなんです)
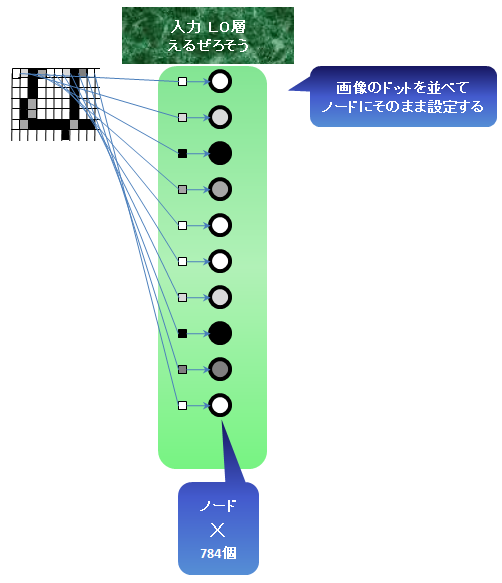
このノードを1列にならべてL0層(えるぜろそう)という仮の名前をつけます。(説明のためです)くどいですが、この時点でいったん、まわりのドットがどうなのかはまったく関係なくなります。順序は重要です。
(2)100個の中間〇(ノード)(例では100個にしているけど、何個でもいいです。ただしゼロはダメです。)入力から読み込んだ情報をつたえてもらうものです。
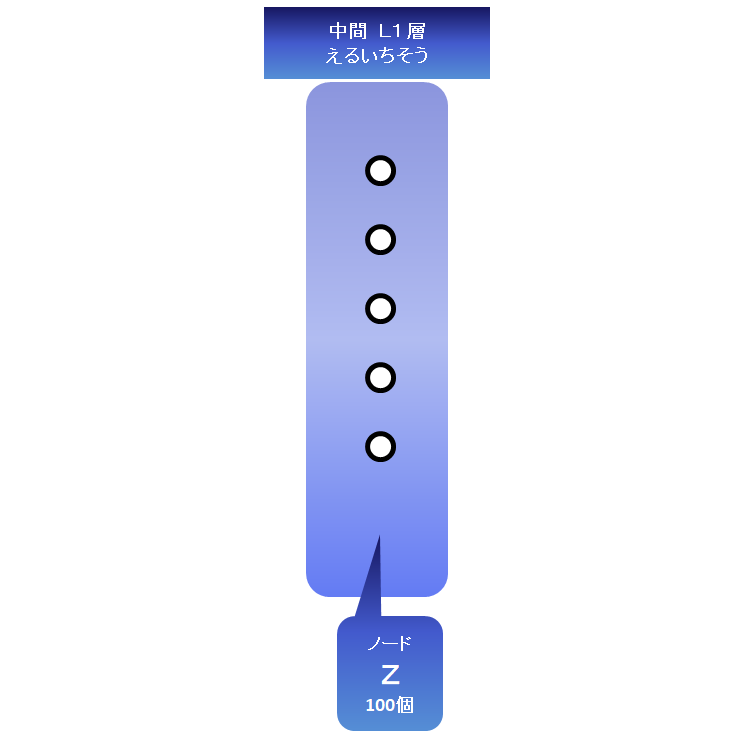
このノードを1列にならべてL1層(えるいちそう)という仮の名前をつけます。(説明のためです)
(3)784個の出力用〇(ノード)
画像を再現して出力するもの(再現された記憶や図形などに相当するもの)
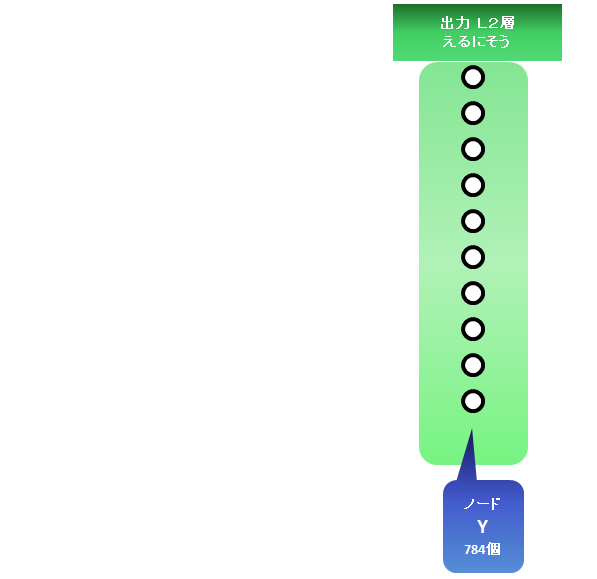
このノードを1列にならべてL2層(えるにそう)という仮の名前をつけます。(説明のためです)
画面に表示するときは784個ある点(ドット)を元の順序と同じにならべて28×28ドットの図形として表示することになります。
(4) (1)と(2)をつなぐ/(エッジ)
784×100本 (784個の入力〇(ノード)と100個の中間〇(ノード)をつなぐよ)
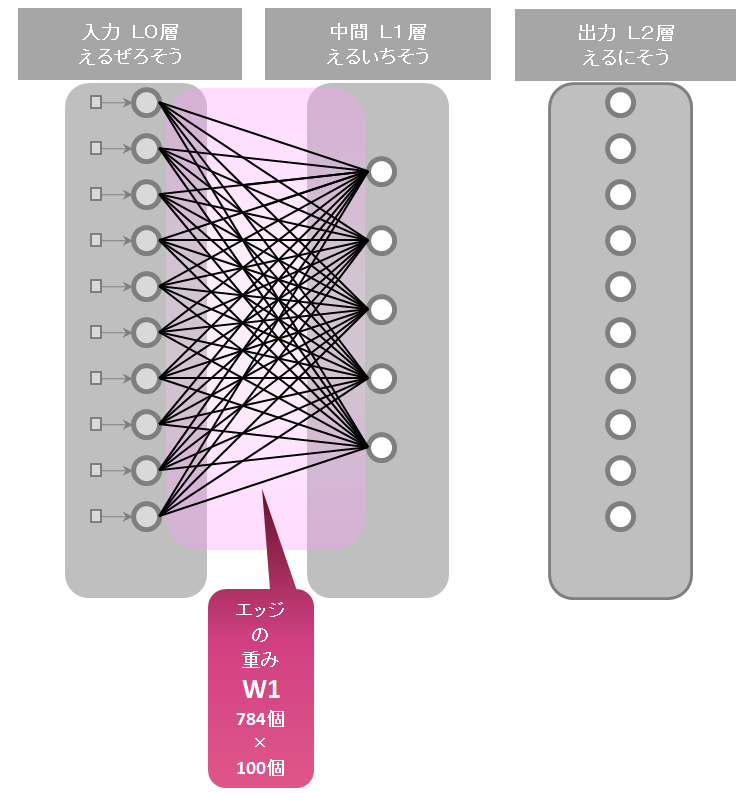
(5) (2)と(3)をつなぐ/(エッジ)
100×784本 (100個の中間〇(ノード)と784個の出力〇(ノード)をつなぐよ)
しくみのための材料
(6) /(エッジ)のつながりの強さをあらわす「重み(W)」の値(/(エッジ)の数ぶん)
784×100本 の/(エッジ)のW1
100×784本 の/(エッジ)のW2
1本の/(エッジ)に1つの「重み(W)」があります。「エッジのつながりがどれだけ強いか」をあらわすと思ってもらえばいいです。「ゼロ」のときは「つながっていないのとおなじこと」になります。
(7) 〇(ノード)の性格(f):熱くなりかた
1個の〇(ノード)に1つの「性格(f)」(せんもん的には活性化関数(f)(かっせいかかんすう)といいます。)
急に熱くなるか、ゆるやかに熱くなるかのような性格(f)を考えます。
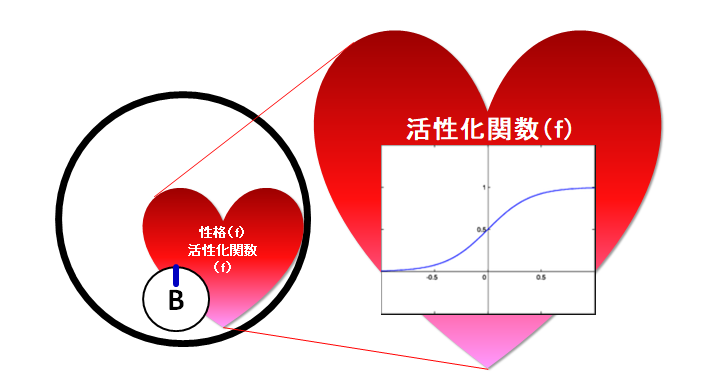
「性格」という言い方はこのページだけの説明上のものです。(たとえです)
「ほどよく急な」ところと「なだからな」ところがある性格の形がよくつかわれます。
図にある「B」の部分はあとからでてくる「バイアス(B)」です。
性格(f):活性化関数(f)ってなに?
たとえばどんな性格(f)の形があるかというと
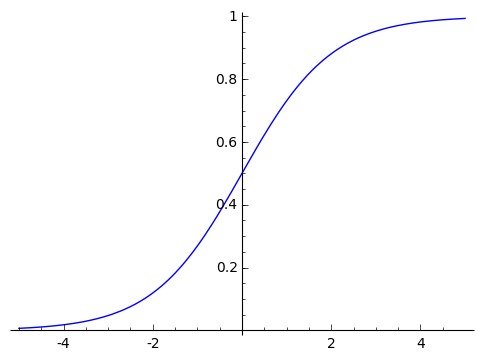
シグモイド関数(かんすう:f)
※なだらかーなところあれば急なところもあるほどよい性格(f)
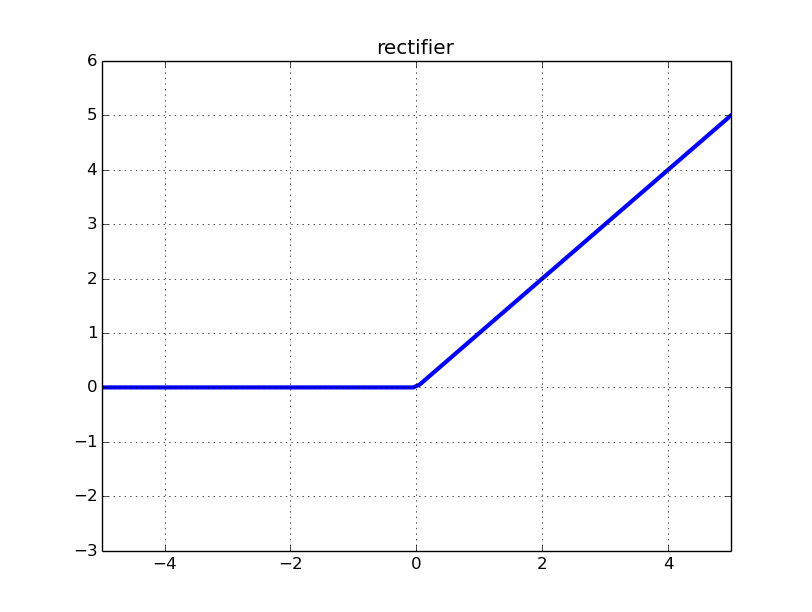
ReLU関数(らんぷ、れるー、あーるいーえるゆー、れくたふぁいあ すきに読んでいいよ:f)
※興味ないときはとことん全く興味ない性格(f)。
リニア関数(恒等関数:こうとうかんすう ともいいます:f)
※はいってきただけ熱くなるよ。わかりやすい性格(f)。
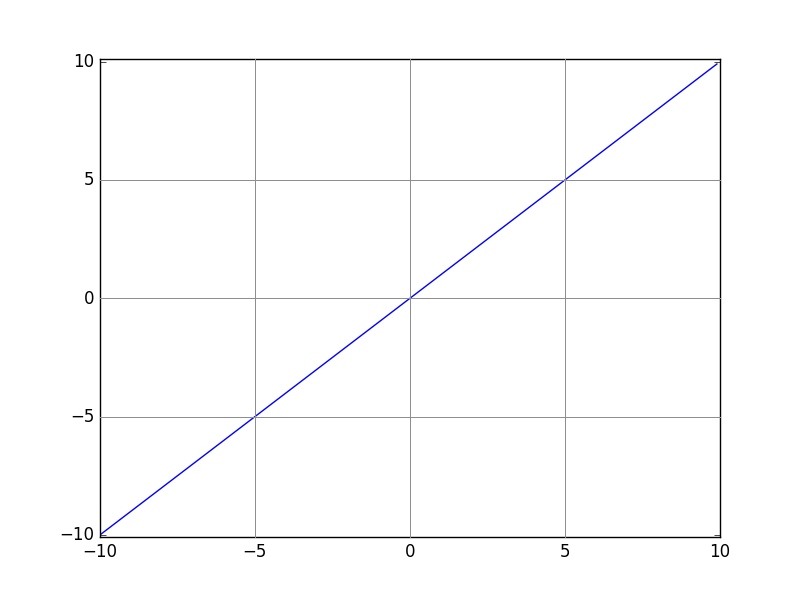
ほかにもたくさんあります。
(8)〇(ノード)のバイアス(B)
敏感(びんかん)なのか鈍感(どんかん)なのか「熱くなりやすさ」を調整(ちょうせい)する「バイアス(B)」というのをかんがえます。バイアスは単に「入力に加えて調整する」と理解するより、「入力に対してどう反応(はんのう)するのか」「グラフを横に動かして、調整する」と理解した方がわかりやすいです。※しきい値自体をかえるのではいことに注意しましょう。
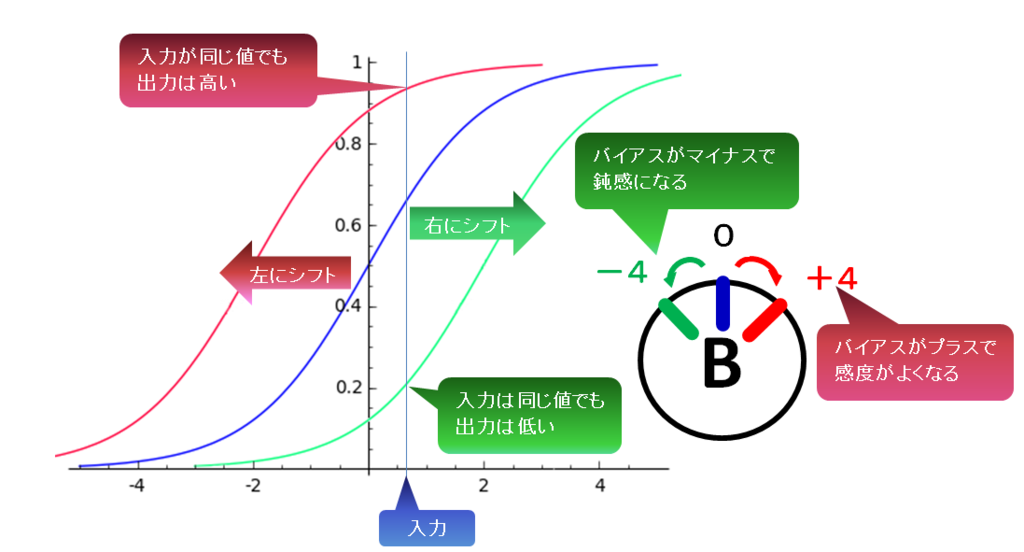
なお、入力層の〇(ノード)は元の画像がはいっているだけなので、「性格(f)」も「バイアス(B)」もありません。(必要ありません)
つないでみよう!
つなぎ方のお約束(ルール)
・いろんなつなぎ方が考えられるけど、今回は「〇」は1列(1層)に並んでいて、並んでいる横(列にならべたら縦)の「〇」とはどれも「/」でつながっていないことにします。
・ある列(L:層)の「〇」は次の列(L:層)の「〇」とは全部「/」でつながっているよ。
・ある列(L:層)にならんでいる「〇」はどれも同じ性格(f)と決めます。
・同じ性格(f)でも敏感なのか鈍感なのかが違い、それ(どらくらい敏感か鈍感か)をバイアス(B)で表します。
・「/」は「〇」から「〇」へ値を伝えますが、「重み(W)」を持っていてたくさん伝わるか、少ししか伝わらないかがかわります。「重み(W)」が大きいと前の〇の熱さの「値」がすくなくても、たくさん伝わるよ。
・それぞれの〇(ノード)は/(エッジ)で伝えられた値と性格(f)によってどれだけ熱くなったかの値を持ちます。
つないでみます
ノードはすべて〇であらわします。
エッジはすべて/であらわします。こんな感じになります。
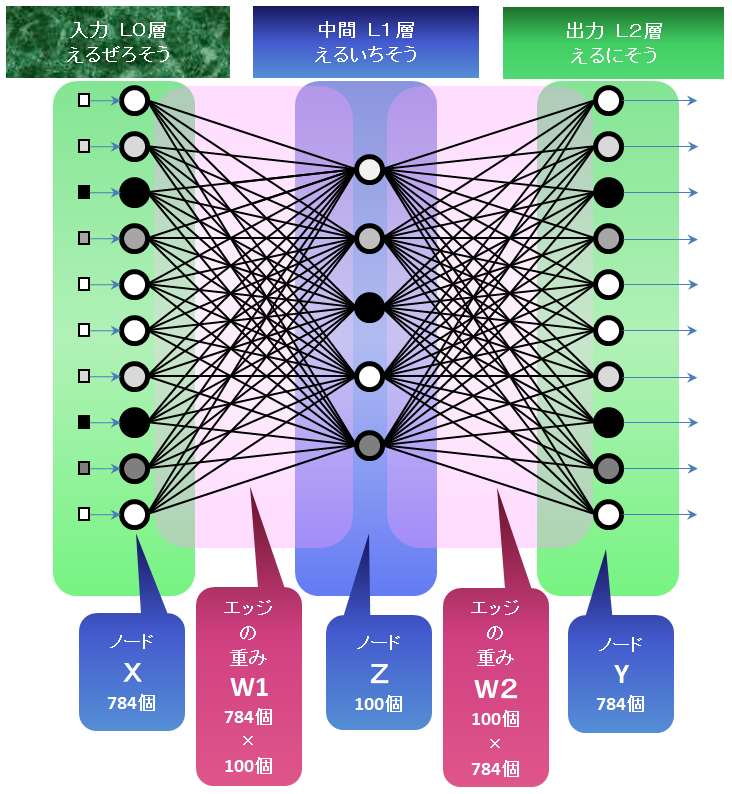
どんなふうに動くのかをみてみましょう。
まずは、全部1個づつで考えてみます
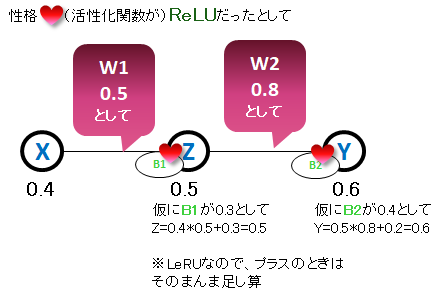
何個かで考えてみます。
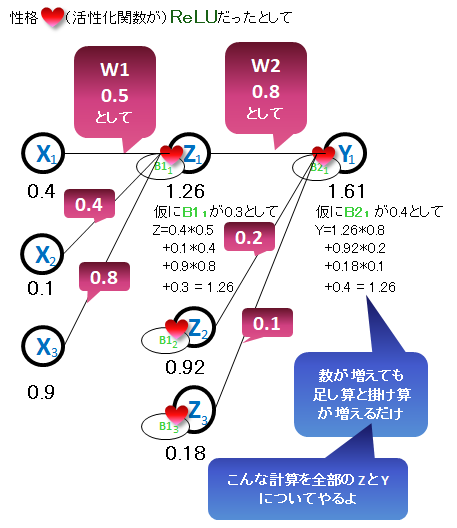
な~んだ。「性格」はともかく、足し算と掛け算しかやってないじゃん。と思ってもらえればうれしいです。
数式って簡単に表すためのもの?伝えるためのもの?
でも掛け算や足し算を何百個、何千回もやるのはやだ!めんどくさい!!
でも昔のめんどぐさがり屋さん(数学者:すうがくしゃとも言います)が簡単にする方法を考えだしました。
ぱっぱら~♪「全部いっぺんにまとめて計算する方法」です。
とにかくまとめて1つにして考える方法です。
入力(L0:えるぜろ層)のノードの値「X」
入力は784個ありましたが、これをまとめて1個であらわす方法は
X(えっくす)
です。Xの中には784個の数字がはいっています。イメージしてみましょう。
ちゃんとならんで入っています。1列に並んで入って入っています。
これを784個ある入力□(ノード)にそのままセットします。
一列の箱の区切り中に数字がはいったものをイメージしてくれたお友達も多いかもしれません。
袋の中に784個のクッキーがはいっているのを想像したおともだちもいるかもしれません。
本棚の中に784冊の本がならんでいるのを思った人もいるかもしれません。
全部OKです。だた、どれも中のものには番号がついていてわかるようになっています。
ひとまとめてしまえば、「1個」で扱えます。「1箱」「1袋」「1本棚」です。
数字や記号だけであらわすと次のようになります。
入力はXエックス
エッジの重み「W」
次に/(エッジ)の部分を考えてみましょう
入力(L0:えるぜろ層)と中間(L1:えるいち層)のつながりは
784×100本
でした。
入力の〇(ノード)が784個で、中間の〇(ノード)を100個にしているから全部線をひくと掛け算になるよね。
(784個ある入力〇ノードからはそれぞれ100本線が引けるから...78,600本だ!)
昔のめんどくさがり屋さん(数学者:すうがくしゃとも言います)はもちろんこれも簡単に1つで扱う方法を考えました。
1個であらわす方法は
W(だぶりゅー)
です。Wの中には784個の行とそれぞれ100個の列があります。
箱の中に784行の横の仕切りがあって、その行の中に100個の縦の仕切りがあって数字がはいっているのをイメージしてくれたお友達も多いかもしれません。
袋の中に784個の小袋がはいっていてその中に100個つづクッキーがはいっているのを想像したおともだちもいるかもしれません。
図書館の中に本棚が784棚あって、そのそれぞれの中に100冊の本がならんでいるのを思った人もいるかもしれません。
全部OKです。だた、どれも中のものには番号がついていてわかるようになっています。
「何行目、何列目」とか「袋番号、その中のクッキー番号(何個目か)」とか「棚番号、そのなかの本番号(何冊目か)」です。
このように中にはいっているものを2つの数字であらわすことができます。(これを数学では2次元行列といいます。)
重みはWダブリュー
中間ノード(L1:えるいち層)の値「Z」
次に中間の〇(ノード)をかんがえましょう。
100個あります。この〇(ノード)にはいってくる(伝わる)値を考えます。
上で出てきた、XとWで考えてみましょう。
伝わる値
X × W です。
エックスと掛け算がわかりにくですね。数学ではエックスをよく使います。掛け算もよく使います。
昔のめんどぐさがり屋さん(数学者:すうがくしゃとも言います)は大発明をしました。
掛け算はよく使うし、いちいち書くのはめんどくさいから、省略しちゃおう!つづて書いたら掛け算したことにしちゃおう!!
こうして人類(じんるい)は「掛け算を省略して書く術(じゅつ)」を習得してレベルアップしました!!!
伝わる値は
XW
と書けます。
これで中間ノード100個分(ということはエッジ784×100本ぶん)の計算を一度に全部考えたことになります!(だって、Xは784個分、Wは784×100個分なので!)おお、行列ってちょー便利。エコです。
でははいってきた全部の値「XW」でそれぞれの中間の〇(ノード)はどれくらいの値になるのでしょうか
数式であらわすと便利なので、昔のめんどくさがり屋さん(数学者:すうがくしゃとも言います)がこんなときどうあわらしたか見てみましょう。
Z=f(はいってきた値+B)
Z(ぜっと)は〇(ノード)がどれだけ熱くなったかの値です。
fは活性化関数といいます。上の説明では「性格」として説明していたものです。
でてくる値=f(入れる値)
のようにあらわします。こんな風に昔のめんどくさがり屋さん(数学者:すうがくしゃとも言います)は計算の方法を簡単(かんたん)に表す表し方をくふうして簡単にできるしくみを考えてきました。
一見(いっけん)めんどくさそうな表し方でも組み合わせたり、応用(おうよう)したりすると実はそれが「簡単」であることがたくさんあります。それに数式は「ことば」でもあり、「あらわし方の全世界共通(ぜんせかいきょうつう)のルール」でもあります。
これを覚(おぼ)えれば外国の人と「数学」で会話ができます。(数式は他の人に考えを伝える共通の言葉であり、また書物(しょもつ)の文書(ぶんしょ)のように後世(こうせい)にもそれを伝えていくものです。そしてなにより自分の考えをまとめるのに便利です)*2
どれくらい笑うか=わらう関数(おもしろいこと)
おもしろいことを言ってどれくらい笑うのかの「性格:関数」をかんがえみましょう。
「わらわない」=わらう関数(「けしゴムころがった」)
「にやけた」=わらう関数(「けしゴムころがった」+「ふとんがふっとんだ」)
「爆笑」=わらう関数(「けしゴムころがった」+「ふとんがふっとんだ」+「ぶどうひとつぶどう」)
でも、ひとによって笑い上戸(じょうご)のひとと、リアクションが薄(うす)い人がいます。
そんなとき、調整をするのがバイアス(B)、別名「下駄(げた)」とかいいます。縦方向に使えば背が高くなります。横方向に使えば、グラフの形が横に移動(シフト)します。
バイアスを使って、笑い上戸の人とリアクションが薄い人を表してみましょう。
笑い上戸の人
(図を書く)
リアクションが薄い人
(図を書く)
問題:「けしゴムころがった」だけで笑う人はどんなバイアスを持った人でしょう。(バイアスはプラス?マイナス?)
100個の〇(ノード)がどれだけ熱くなるか(活性化するか)は下の式であらわされます。
Z=f(XW+B)
ここでBはそれぞれの〇(ノード)のバイアスです。バイアスは入力ではありません!それぞれの〇(ノード)で固有にもっている関数のはたらき具合を調整するものです。重さでもありません。また、/(エッジ)が持っている値ではありません!〇(ノード)が固有にもっている(そして〇(ノード)のもつ関数にくっついている)値です。ここは特に勘違(かんちが)いしやすいので注意しましょう。
急に難(むずか)しくなった気がする人もいるかもしれませんが、表し方をかえただけです。昔のめんどくさがりな人がわざわざ難しくしていることはないんです。要(よう)は慣(な)れです。言葉であらわすとこんな感じです。
それぞれの人がどれだけ笑うか=わらう関数(ぜんぶのおもしろ話(のおもしろさ)+それぞれの人の笑いやすさを調整する値)
つぎのエッジの重み「W2」
次に中間(L1:層)から出力(L2:層)への重みW2を考えましょう。(最初のWはW1にしちゃいましょう)
ちょっとした「発想(はっそう)の転換(てんかん)」(ちがったみかたをすること)が必要です。
どうやったら少ない100個の値から元の784の値を復元できるのでしょうか?
普通に考えると100個になってしまった値が784個になることはありません。
でもみんなで力をあわせればできるかもしれません。きっとできるはずです!
ちょっとするします。カンニングともいいます。
入力(L0:えるぜろ)層を中間(L1:えるいち層)で折り返して出力(L2:えるに層)にします。
そうすれば一旦中間で少なくなったノード「数」をもとのノードの「数」に戻して、元のノードの中にはいっていた値を復元できるかもしれません。ここで、「カンニング」(ずる)といっても元の値をそのままコピペするのではなく、つながり方や重みをコピペします。実はこうすることによって(で)も、ほどよく元にもどせることがあります。
やってみましょう。(かんにんぐ)
W1をW2にコピペ。。。できません。
W1は784×100のエッジの重み
W2は100×784のエッジの重みで総数は同じですが、形が違います。
どうすればいいのでしょうか。むりやりコピペする方法はないでしょうか。
じつは線対称でひっくりかえす考えなので、W1をひっくりかえして複写すればいいのです。
W1をひっくりかえす?そうです。行と列をひっくりかえします。
そうすれば、W1は784行100列から100列784行になるので、W2にばっちり「はめこむ」ことができます。
この行と列をひくりかえすことを転置(てんち)といいます。
W1をひっくりかえして書くのはむずかしいのでにするとわからなくなるので、 と書きます。例をみてみましょう
(例を書く)
とりあえずここでは
W2=W1T
としておきます。これを専門的には「重み共有(きょうゆう)」といいます
まぁ、ちょっとしたずる(手抜き:てぬき)です。
出力(L2:えるに層)の値「Y」
さて、最後の層になりました。出力(L2:えるに層)をみてみましょう。
前の中間層の〇(ノード)の値「Z」を使って計算してみましょう。
出力はY(わい)を使ってみます。
Y=f(ZW2+B2)
W2とB2は別に2をかけているわけではなくて、2ばんめ(の部分)という意味です。「W2」で1文字のように考えてください。W2もB2も例によって「ぜんぶをいっぺんにあらわす」行列を使っているよ。B2は出力(L2:えるに層)のノード768個あるので、B2の行数も768個あるよ。中間層用のB1(中身は100個)とB2(中身は784個)は折り返し(重み共有)で複写できません。(最初のB2もでてきたので、WでやったようにBをB1とあらわします。)
重みはひっくり返して(転置(てんち)して)使うけど、バイアスは共有しません。だから「重み共有」で「バイアス」は関係ないのです。
これで、入力784個から100個に圧縮して、784個に戻しました。
たとえば入力784個から100個にすること、符号化(ふごうか:エンコード:べつの形であらわすこと)
100個から784個へ出力することを、復号化(ふくごうか:デコード:元の形にもどすこと)といいます。
これで使えるの?
さてこれで本当にいったん別の形であらわしたものがもとに戻るのでしょうか。
じつは、まだもとに戻せないのです。WとBの値をいい値にきめないといけません。
苦労してやってきましたが、まだゴールは遠いのです。
次のことが必要です。
・図形などをちゃんと戻せるように「W1とW2の値を決める」
・図形などちゃんと戻せるように「B1とB2の値を決める」
なんだ4つじゃん。あれ?
W1とW2はそれぞれ784×100=78400個、100×784=78400個
B1とB2はそれぞれ100個と784個あります。
けどW2は「ずる」(エコ、効率化)してW1をひっくりかえして複写するのでW1の78400個
だから合計79,268個の値を決めないといけません。4個じゃなかった!
えっ!?まだ続くの?
どうやってきめればいいのでしょうか。次は「教師:きょうし(せんせい)」という考えかたがでてきます
もう少しがんばってみたいお友達は次の「ノードは気長に学習していく編」をみてくだい。乞うご期待(するほどではないです)
(参考)
行列をかけるときはきまりがあります。
前のほうの行と次の列が「同じ数」そろっている必要があります。つながる相棒がいないと計算できません(つながりません)
入力〇 /エッジ 中間〇 /エッジ 出力〇
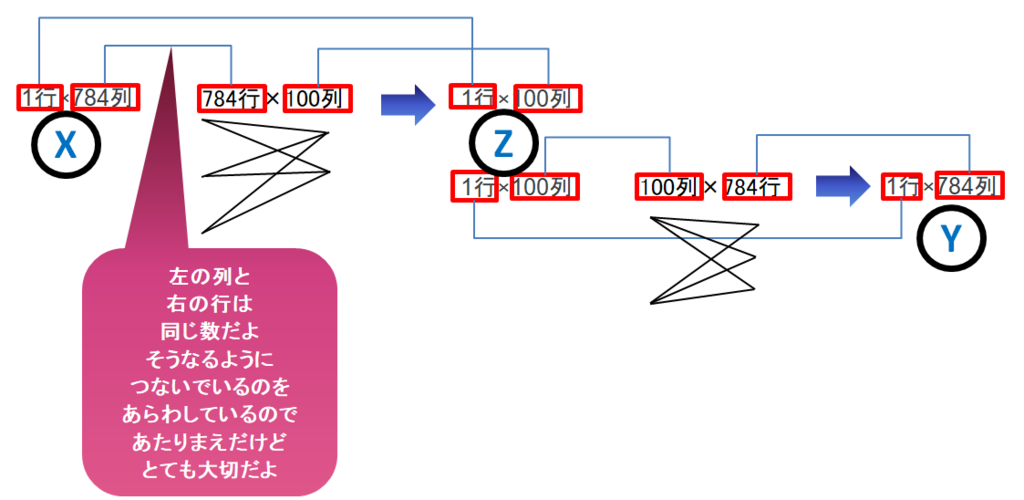
「行列」のことは「イメージ」しか書かなかったけど、高校の数学でならいます。
たのしみにしていてね。
(追記:注意)すみません、高校ではいまは「行列」ないそうです。そのかわり複素数(ふくそすう)をたくさんならうようです。え~ほんとかな?ボクハ行列、習いましたよ?理系?の高校ではならうのかな?いやぁ、日本がAI(えーあい:じんこうちのう)がんばるんなら、まず「行列」を復活(ふっかつ)させないとダメでしょ。VRで3Dもさかんなので、3D計算するなら必須(ひっす:かならずひつようなこと)ですし。(でも複素数もとっても大事ですね。電磁気学(でんじきがく)とか量子力学(りょうしりきがく)やるならこちらですね。波を扱ったとたん複素数が大活躍(だいかつやく)です。)こんど、文部科学省(もんぶかがくしょう)に高校で「行列」を復活させるようメールしておきます。(ウソで~す。)機械学習(きかいがくしゅう)を「本気(マジ)」で勉強したいお友達は大学のおにーさん、おねーさんに教えてもらうか、大学までお待ちください。まぁ、そういうボクモ「コレ習っても絶対、一生使うことはない」と思っていたのを告白(こくはく:「愛してます」ではなく「ゲロ」の方)します。今は、毎日コレばっかりです。(追記:ここまで)
最後までよんでくれて本当にありがとう
実は本当によんでくれている「おたまじゃくし」や「小中学校のお友達」がとっても少ない気配(けはい)を感じています。(書いている「かえる」や「人」は、どんな人が読んでくれているのか正確(せいかく)にはわかりませんが「傾向」(けいこう:だいたいのかんじ)はなんとなくわかります)でも1人でも、「最後まで読んでもらえるお友達がきっといる」と信じて次もがんばります。